Matriz Booleana
Una matriz es un arreglo rectangular de números dispuestos en m reglones horizontales y n columnas verticales, cuyos elementos son 0 y 1 .Es por esto que se dice que las matrices booleanas tienen un orden de mxn.
Matriz de operaciones booleanas
Las
operaciones que se pueden realizar entre matrices booleanas son tres: unión,
conjunción y producto booleano. Estas operaciones no pueden
realizarse sobre dos matrices cualesquiera, sino que deben cumplir ciertos
criterios para poder llevarse a cabo. En particular, en el caso de la unión y
la conjunción, las matrices que intervienen en la operación deben tener el
mismo tamaño, y en el caso del producto booleano, las matrices deben cumplir
con las mismas condiciones que para formar el producto de matrices.
Unión / Disyunción

Intersección / Conjunción

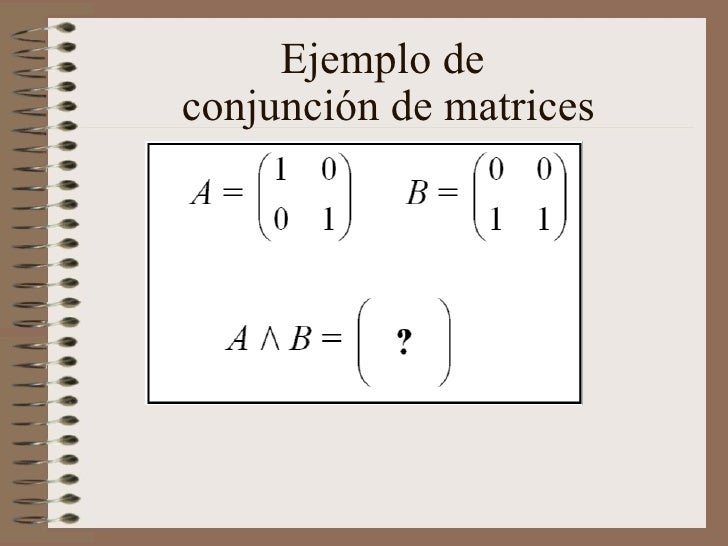






Producto booleano:
El producto booleano de las matrices A=[aij] y B=[bij], órdenes mxk y kxn respectivamente, se denotado por A O B. Este producto es la matriz mxn cuyo elemento (i,j ) es cij, donde:
 Otras operaciones matriciales
La traspuesta de una matriz booleana es también
otra matriz booleana; pero las operaciones con matrices booleanas no siempre
producen matrices booleanas.
Otras operaciones matriciales
La traspuesta de una matriz booleana es también
otra matriz booleana; pero las operaciones con matrices booleanas no siempre
producen matrices booleanas.

Matriz booleana asociada a una relación
Ejemplos:

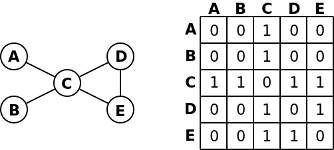
El grafo
no-dirigido de la figura adjunta puede entenderse como una relación binaria.
Dos elementos están relacionados si existe una línea que los una directamente.
La matriz asociada a la relación binaria de conexión directa se llama matriz de incidencia, que es una matriz booleana que viene dada por:
 El elemento ij
de la anterior matriz es 1 si existe una línea que una directamente los círculos
i y j y 0 en caso contrario
El elemento ij
de la anterior matriz es 1 si existe una línea que una directamente los círculos
i y j y 0 en caso contrario


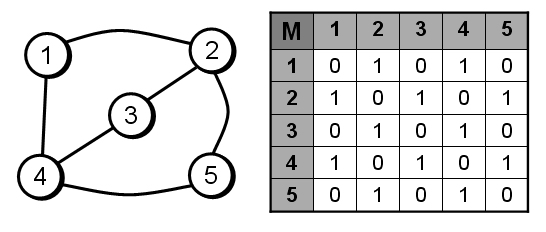
El grafo no-dirigido de la figura adjunta puede entenderse como una relación binaria. Dos elementos están relacionados si existe una línea que los una directamente. La matriz asociada a la relación binaria de conexión directa se llama matriz de incidencia, que es una matriz booleana que viene dada por: